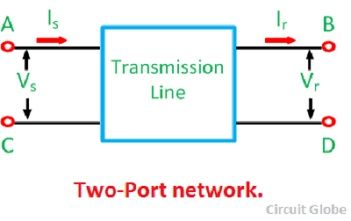
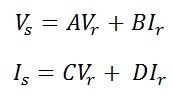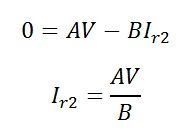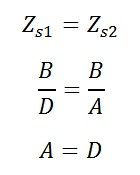Transmission of power from generating unit to distributing units can be done through the transmission line. During transmission, many losses occur in the transmission line which decreases the efficiency of a line. For improving the proficiency of the transmission, two port networks are used.
A network having two input and two output terminals is known as a two port network. The network shown below has four terminals in which A and B represents the input port where as C and D represents the output port.
The voltage and current in the output and input terminals of a two-port network are given by the equations shown below
Vs = sending end voltage
Is = sending end current
Vr = receiving end voltage
Ir = receiving end current
A, B, C and D are the constants also known as the transmission parameters or chain parameters. These parameters are used for the analysis of an electrical network. It is also used for determining the performance of input, output voltage and current of the transmission network.
The above equations can also be written in a matrix form for easy calculations shown below
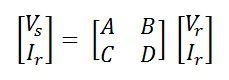The matrix 
is called the transfer or transmission matrix of the network.
ABCD parameters for open circuit
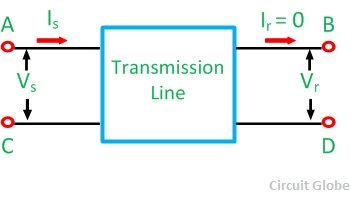In the open circuit, the output terminals are open, and the voltage measure across them is Vr. Since the circuit is open at the receiving end, the current Ir remains zero.
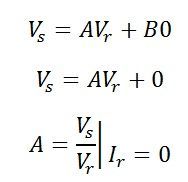From above equations, we get the value of A parameter which is the ratio of sending end voltage to the receiving end voltage. It is a dimensionless constant because their ratio has the same dimension.
Similarly, if Ir =0 is substituted in current equation,
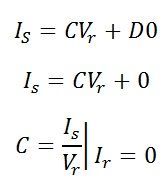we get the value of c parameter which is the ratio of the sending end voltage to the current. Its unit is Siemens.
ABCD parameters for short circuit
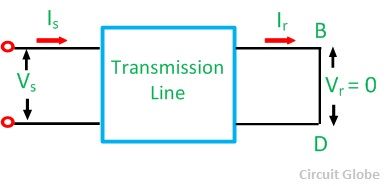For the short circuit, the voltage remains zero at the receiving end.
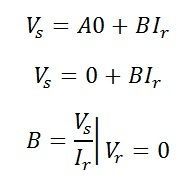If we put Vr = 0 in the equation, we get the value of B which is the ratio of sending end voltage to the receiving end currents. Its unit is ohms.
Similarly, if we put Vr= 0 in current equations,
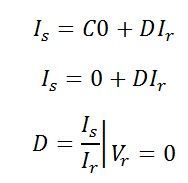we get the value of D, which is the ratio of the sending current to the receiving current. It is the dimensionless constant.
Relation between ABCD parameters
For determining the relation between various types of network, like passive or bilateral network reciprocity theorem is applied. The voltage V is applied to the sending end, and the receiving end is kept short circuit, so the voltage becomes zero.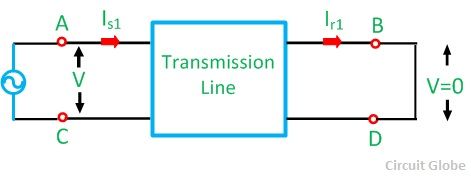 
Since, under short circuit the receiving end voltage is zero, the voltage and current equations become
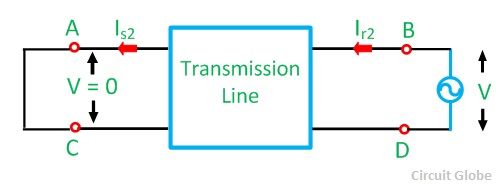
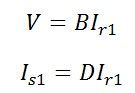Similarly, the voltage is applied at the receiving end, and the input voltage remains zero. Thus, the direction of the current in the network changes, which is shown in the diagram below
The sending end voltage becomes zero. The current flows through the receiving end is given by the equation
and
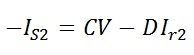Consider, the network is passive, i.e. it contains only passive components in the circuit like inductance, resistance, etc. So the current remains same Is = Ir.
Combining the above equations give,
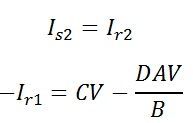dividing the above equation from -V/B we get,
This relation helps in determining the fourth parameters if we know any three parameters.
For a symmetrical network, the input and output terminal may be interchanged without affecting the network behaviour.
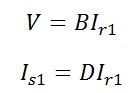If the network is supplied from input terminals and an output terminal is short circuit, then the impedance becomes
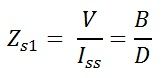
and if the supply is from the output terminal and an input terminal is a short circuit then the impedance becomes
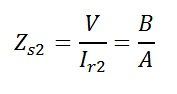in the symmetrical network, the impedance remains the same
